MECÂNICA GRACELI GENER. - QUÂNTICA DIMENSIONAL TENSORIAL RELATIVISTA DE CAMPOS [777]

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

[

$\psi ^{*}$

$TeoriaInteraçãomediadorMagnitude relativaComportamentoFaixaCromodinâmicaForça nuclear forteGlúon10411/r71,4 × 10-15 mEletrodinâmicaForça eletromagnéticaFóton10391/r2infinitoFlavordinâmicaForça nuclear fracaBósons W e Z10291/r5 até 1/r710-18 mGeometrodinâmicaForça gravitacionalgráviton101/r2infinito$

Teoria	Interação	mediador	Magnitude relativa	Comportamento	Faixa
Cromodinâmica	Força nuclear forte	Glúon	1041	1/r7	1,4 × 10-15 m
Eletrodinâmica	Força eletromagnética	Fóton	1039	1/r2	infinito
Flavordinâmica	Força nuclear fraca	Bósons W e Z	1029	1/r5 até 1/r7	10-18 m
Geometrodinâmica	Força gravitacional	gráviton	10	1/r2	infinito

$G* = OPERADOR DE DIMENSÕES DE GRACELI.$

DIMENSÕES DE GRACELI SÃO TODA FORMA DE TENSORES, ESTRUTURAS, ENERGIAS, ACOPLAMENTOS, , INTERAÇÕES E CAMPOS, DISTRIBUIÇÕES ELETRÔNICAS, ESTADOS FÍSICOS, ESTADOS QUÂNTICOS, ESTADOS FÍSICOS DE ENERGIAS DE GRACELI, E OUTROS.

Os polinômios de Hermite são um exemplo de polinômios ortogonais cujo principal campo de aplicação encontra-se na mecânica quântica, especialmente no estudo do oscilador harmônico unidimensional. São nomeados assim em homenagem a Charles Hermite.

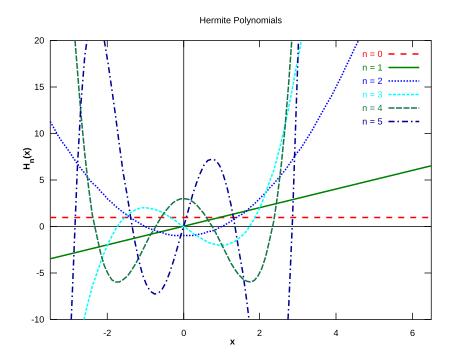
Definição

Os polinômios de Hermite ("polinômios de Hermite probabilísticos") são definidos por:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

H_{n}(x)=(-1)^{n}e^{x^{2}/2}{\frac {d^{n}}{dx^{n}}}e^{-x^{2}/2}\,\!

Ou, às vezes, por ("polinômios de Hermite físicos")

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

H_{n}^{\mathrm {phys} }(x)=(-1)^{n}e^{x^{2}}{\frac {d^{n}}{dx^{n}}}e^{-x^{2}}\,\!

Essas definições não são exatamente equivalentes: uma é o redimensionamento da outra:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

H_{n}^{\mathrm {phys} }(x)=2^{n/2}H_{n}^{\mathrm {prob} }({\sqrt {2}}\,x)\,\!

Os polinômios físicos podem ser escritos como:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

H_{n}^{\mathrm {phys} }(x)=(2x)^{n}-{\frac {n(n-1)}{1!}}(2x)^{n-2}+{\frac {n(n-1)(n-2)(n-3)}{2!}}(2x)^{n-4}-\dots

Propriedades

Ortogonalidade

H_n(x) é um polinômio de grau n, com n = 0, 1, 2, 3 ... . Esses polinômios são ortogonais com relação à função peso

e^{-x^{2}/2}\,\!

(probabilidade)

e^{-x^{2}}\,\!

(física)

ou seja,

\int _{-\infty }^{\infty }H_{n}(x)H_{m}(x)\,e^{-x^{2}/2}\,dx

\int _{-\infty }^{\infty }H_{n}(x)H_{m}(x)\,e^{-x^{2}}\,dx={n!2^{n}}{\sqrt {\pi }}~\delta _{\mathit {nm}}

(física)

onde $\delta _{\mathit {nm}}$ é o delta de Kronecker, que é igual à unidade quando $n=m$ e nulo no caso contrário. Os polinômios probabilísticos são ortogonais em relação à função densidade de probabilidade normal.